Biological, Soft Matter, Nonlinear, and Statistical Physics

Biological Physics

Biological physics is by definition an interdisciplinary science where ideas and techniques from physics are utilized to understand biological systems and phenomena. Biological materials are classed as soft materials and there is a natural synergy between these disciplines. The unique academic structure at UC Merced is especially conducive to research in biophysics with collaborations between faculty across physics, chemistry, biology, applied math and bioengineering disciplines. The biophysics group at UC Merced has a wide variety of research interests including:

• macromolecular transport (Gopinathan)

• structure and function of cell membranes (Hirst, Xu)

• biopolymers- structure, dynamics and function (Gopinathan, Hirst, Dasbiswas, Xu)

• biophotonics (Sharping)

• bacterial physics - growth, division, motility (Gopinathan, Liu)

• molecular motors, intracellular mechanics and transport
  (Xu, Gopinathan, Dasbiswas)

Soft Matter Physics

Soft matter science (or soft condensed matter) is the study of materials that are neither crystalline solids, nor simple liquids — they are somewhere in between. This interesting state of matter can take many forms and can be seen everywhere in the world around us. Some everyday examples of soft matter include, soaps, paints, gels, plastics, liquid crystals and most of your own body and the food you eat. At UC Merced, we are building a group of faculty interested in problems related to soft materials, from new liquid crystal composite materials, to granular media and cell membranes. 

Focus areas include:

• liquid crystals (Hirst)

• polymer physics and elasticity (Gopinathan, Dasbiswas)

• fluid dynamics and granular systems (Liu, Utter)

• membranes (Hirst)

• geometry and topology in soft matter and fluids (Kleckner)

• soft matter education (Utter)

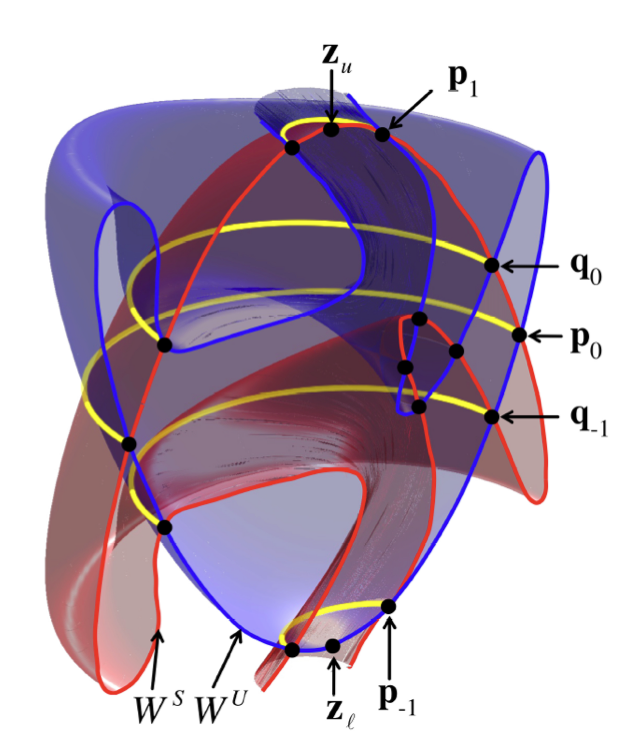
Nonlinear and Statistical Physics

Most processes encountered in nature are inherently nonlinear, meaning that nonlinear dynamics finds applications across a wide range of disciplines from mathematics and physics to chemistry, biology, and engineering.  As such, UC Merced Physics faculty from various subfields share a common bond with their interest in nonlinear phenomena and statistical physics. 

Focus areas include:

• chaotic dynamics in atomic systems (Mitchell)

• nonlinear optics in semiconductor nanostructures (Scheibner) and fiber devices (Sharping)

• thermal transport in DNA (Chien)

• collective phenomena in swarming and foraging (Gopinathan)

• anomalous transport in complex environments (Gopinathan)

• fundamental studies of topological dynamics (Mitchell)